Understanding the Specral Graph Laplacian

Josh Mitton, 2 Feb 2020

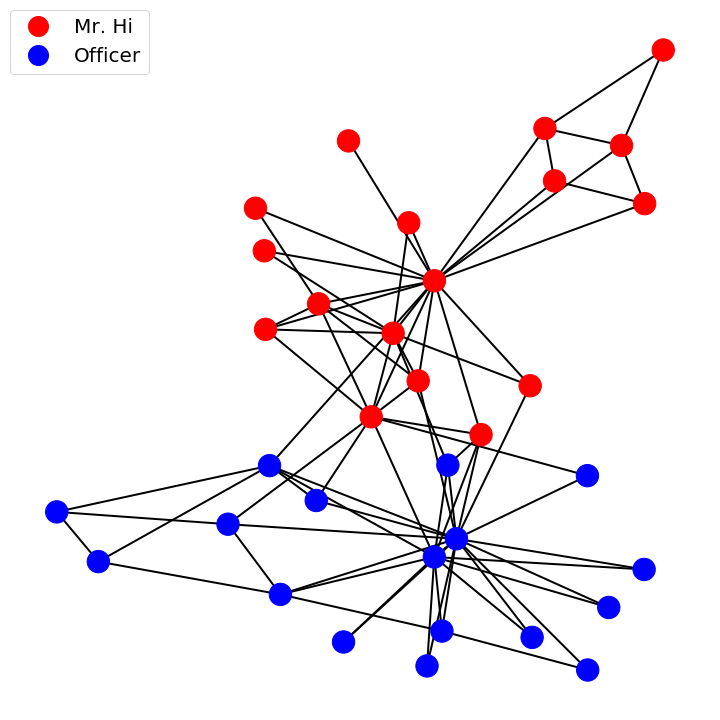
For an introduction to functions defined on graphs that are useful for understanding graph neural networks Zachary's karate club is used as the example graph. This graph is formed from 34 members of a university karate clubs social network. This graph is interesting to compare functions on graphs as the club split into two groups after a conflict; therefore graph nodes, \(X\), represent the group joined following the conflict and graph edges, \(E\), represent friendships before the splitting of the club, forming a graph, \(G=(X, E)\).

Gradients on graphs

The gradient function gives the direction of steepest increase. On a graph this is the direction of steepest increase between nodes. In the case of discrete node labels with two states, as in the karate club, the gradient function gives edges where there is a difference between adjoining node labels.

In the case of the karate club colouring the edges by there respective gradient values highlights friendships that existed between two members who went on to join different groups after the group split.

The gradient function maps from graph nodes to graph edges. It can be intuitively interpreted as the difference between the function evaluated at two points or in the case of the graph two nodes, \(X_i\) and \(X_j\)

\(\nabla: \mathcal{F} (\mathcal{V}) \rightarrow \mathcal{F}(\mathcal{\varepsilon}) \)

\(\ (\nabla f)_{ij} = f_i - f_j \)


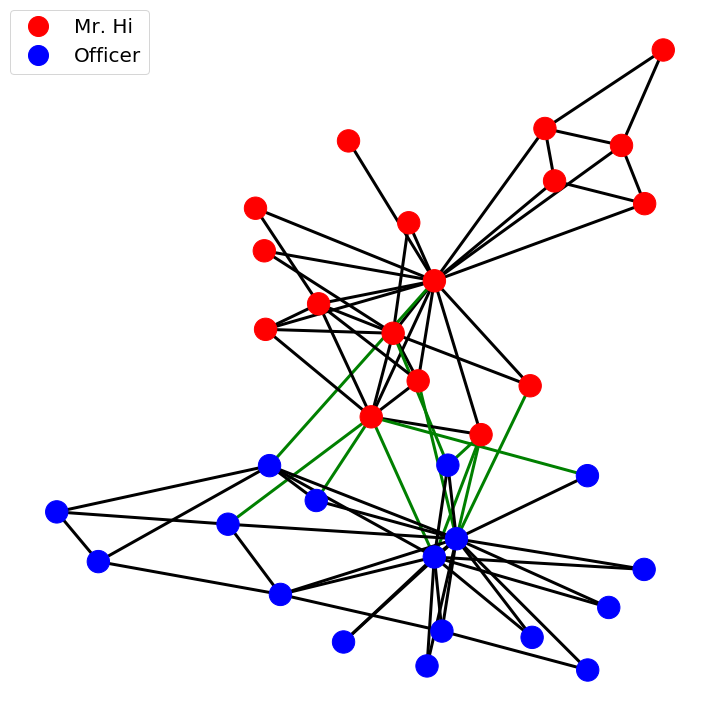
In addition to the intuitive interpretation, the gradient function on a graph can be defined from an incidence matrix, \(K\), whose transpose maps functions over vertices to edges. The matrix \(K\) is an \( (A,B) \) matrix, with \(A\) and \(B\) the number of nodes and edges respectively. To construct \(K\), for every edge, \(e=(i,j)\), \(K_{i,e} = +1\) and \(K_{j,e} = -1\).

\(\nabla: \mathcal{F} (\mathcal{V}) \rightarrow \mathcal{F}(\mathcal{\varepsilon}) \)

\(\ (\nabla f)_{ij} = K^{T} f \)



Divergences on graphs

The divergence of a function represents the density of an outward flux of the function from an infinitesimal volume around a given point. In the case of a graph the infinitesimal volume becomes the sum over neighbouring nodes of the outward flux of the edge function. On a graph with edges representing a constant function, i.e. friendship in the case of the karate club, the divergence becomes the number of neighbours of the node.

\(\nabla: \mathcal{F} (\mathcal{\varepsilon}) \rightarrow \mathcal{F}(\mathcal{V}) \)

\( \mathrm{div} F_{i} = \dfrac{1}{a_i} \sum_{j:(i,j) \in \varepsilon} w_{ij} F_{ij} \)

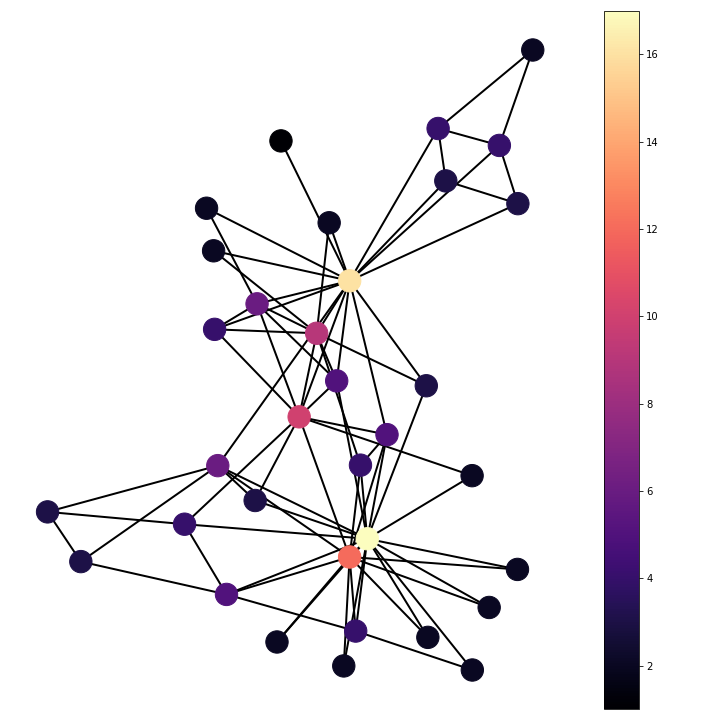
Similarly to the definition of the gradient function, the divergence on a graph can be defined in terms of an incidence matrix, \(K\). The matrix \(K\) is defined in the same way as it was when computing the gradient function.

It should be noted that the divergence values are double that given by the more intuitive method. This is due to the definition using incidence matrices operating on directed graphs, while the previous definition operates on undirected graphs. This yields twice the number of edges using the incidence definition.

\(\nabla: \mathcal{F} (\mathcal{\varepsilon}) \rightarrow \mathcal{F}(\mathcal{V}) \)

\( \mathrm{div} F_{i} = K f \)



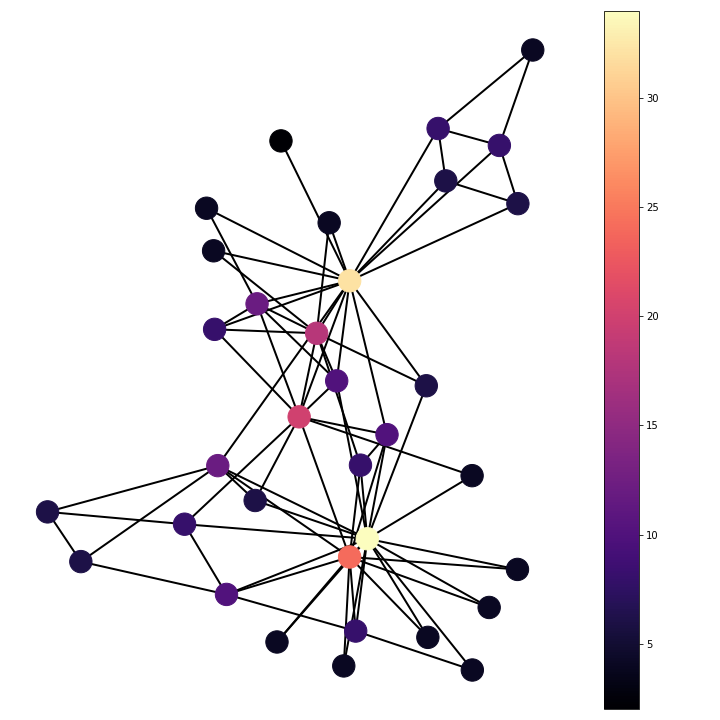
Laplacians on graphs

The Laplacian is the equal to the negative divergence of the gradient function. This is equal to the difference between the gradient function evaluated at a point and the average of the gradient function on a infinitesimal sphere around the point. In the discrete case of a graph the infinitesimal sphere becomes the sum over neighbouring nodes. The Laplacian then becomes the sum of the gradient function scaled by the associated edge weight between the two nodes evaluated over neighbouring nodes.

\(\nabla: \mathcal{F} (\mathcal{V}) \rightarrow \mathcal{F}(\mathcal{V}) \)

\( (\Delta F)_{i} = \dfrac{1}{a_i} \sum_{j:(i,j) \in \varepsilon} w_{ij} (f_i - f_j) \)

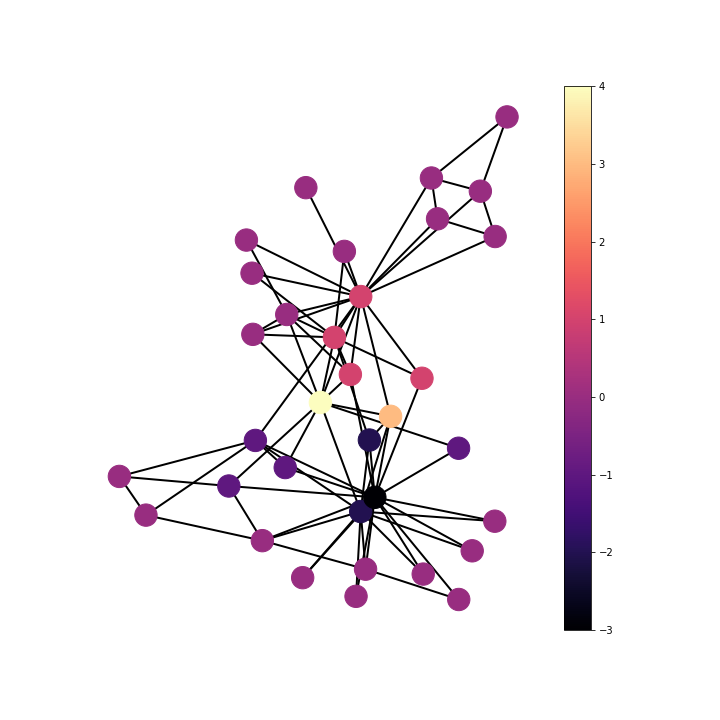
The Laplacian function on a graph can also be defined in terms of an incidence matrix, \(K\). The matrix \(K\) is defined in the same way as it was when computing the gradient function. It should be noted that the Laplacian values are double that given by the more intuitive method. This is due to the definition using incidence matrices operating on directed graphs, while the previous definition operates on undirected graphs. This yields twice the number of edges using the incidence definition.

\(\nabla: \mathcal{F} (\mathcal{V}) \rightarrow \mathcal{F}(\mathcal{V}) \)

\( (\Delta F)_{i} = \mathrm{div} (\mathrm{grad} (f)) = K K^{T} f \)

Finally, another definition of the graph Laplacian is given in spectral graph theory. In spectral graph theory the graph Laplacian if given in the equation below, with a further definition of the Laplacian normalised by the degree matrix of the graph.

\( \Delta = \mathrm{D} - \mathrm{A} \)

The Laplacian definitions given yield the same results demonstrating the three definitions amount to the same Laplacian. The first given is an intuitive example that can be seen to follow from the standard definition of the Laplacian in a Euclidean domain. Following from this, the definition given using an incidence matrix can be seen to equate to the same values as that from the intuitive example. This definition using an incidence matrix also corresponds to the same values when looking at gradients and divergence allowing comparison between the more intuitive method and the incidence matrix method. In addition to equating to the same values, the definition given by an incidence matrix allows the operator, \(K K^{T}\), to be extracted easily and looked at without being applied to the function over vertices. Finally, the definition given by spectral graph theory can be seen to also produce the same results allowing understanding to be drawn from the more intuitive method and applied to the spectral method commonly using in graph theory. Extracting the operator allows for comparison to the incidence matrix method demonstrating that \( D - A = K K^{T} \).

The Laplacian operator on the karate club shows the number of friendships each person had with someone who joined the opposite group after the group split. This can be seen from the definition of the Laplacian as the divergence of the gradient function. The gradient function maps from nodes to edges giving value to edges where there is a friendship spanning a difference in end group choice and zero where the friendship pair join the same group. The divergence is then summing for each member/node over adjoining edge functions, the gradient values, to give the Laplacian. This summation over adjoining edge functions is summing the friendships that spanned different groups after the club split. From this it can be seen that nodes with large positive Laplacian value are people who ultimately joined the group of Mr. Hi, but had many friendships with members who joined the group of Officer; on the other hand, nodes with large negative Laplacian were people who ultimately joined the group of Officer, but had many friendships with members who joined the group of Mr. Hi.